
Remember Volume of all prisms and cylinders is found by. The Volume of a prism is the area of one end times the length of the prism. Triangular prism volume In the triangular prism calculator, you can easily find out the volume of that solid. All cross-sections parallel to the base faces are the same triangle.Īs a semiregular (or uniform) polyhedron Ī right triangular prism is semiregular or, more generally, a uniform polyhedron if the base faces are equilateral triangles, and the other three faces are squares. If all six faces of a rectangular prism are squares, it is a cube.

A uniform triangular prism is a right triangular prism with equilateral bases, and square sides.Įquivalently, it is a polyhedron of which two faces are parallel, while the surface normals of the other three are in the same plane (which is not necessarily parallel to the base planes). A right triangular prism has rectangular sides, otherwise it is oblique. When we find out how much milk is in the container, how much soup is in the can, and how much chocolate is in the packet, we are finding the volume of prisms and cylinders.In geometry, a triangular prism is a three-sided prism it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides. When we find out how much cardboard there is in the box, when we need the area of the walls to paint in a room, or when we need to find how much tin is needed to make a can, we are finding the surface area of prisms and cylinders. We encounter prisms and cylinders everywhere most boxes are rectangular prisms, most rooms are rectangular prisms, most cans are cylinders. Naming prisms and cylindersĪ prism is named by the shape of its base.Ī rectangular prism has a rectangular base and hence a rectangular cross-section.Ī triangular prism has a triangular base and hence a triangular cross-section.Ī cylinder has a circular base and hence a circular cross-section. If we cut or saw through a prism parallel to its base, the cross-sectional area is always the same. The word 'prism' comes from the Greek word that means 'to saw'. In a rectangular prism, the cross-section is always a rectangle. So the area of each slice is always the same. We know that the triangular prism base is in a triangular shape, the area of the base is similar to that of a triangle. For example, if the base is 8 and the height is 9, you would get x 8 x 9 36. J Need help with finding the volume of a triangular prism Youre in the right placeWhethe. To calculate the volume of a triangular prism, first you need to find the area of one of the triangular bases by multiplying by the base of the triangle and by the height of the triangle. In this case the base is a triangle so we simply need.
Volume of triangular prism with circular base how to#
The base of the cylinder is a circle with radius, so. Welcome to How to Find the Volume of a Triangular Prism with Mr. The volume of any prism is the product of the area of the base and the distance between the two bases. This means that when you take slices through the solid parallel to the base, you get polygons congruent to the base. Summary The volume of a rectangular prism is a result of multiplying the area of its base by its height. This is the surface area of all sides of the prism that are not the base. Visual in the figure below: You need two measurements: the height of the cylinder and the diameter of its base. Volume of all types of pyramids Ah, where h is the height and A is the area of the base. The formula is, where equals the surface area of the prism, equals the lateral area of the prism, and equals the area of one base. The volume formula for a cylinder is height x x (diameter / 2)2, where (diameter / 2) is the radius of the base (d 2 x r), so another way to write it is height x x radius2. We will generally say 'prism' when we really mean 'right prism'. Set up the formula for finding the surface area of a prism. Find the volume of the right regular hexagonal prism. This means that when a right prism is stood on its base, all the walls are vertical rectangles. triangular prism with height 20 cm and base edges of length 10 cm. Volume is the amount of space occupied by an object.

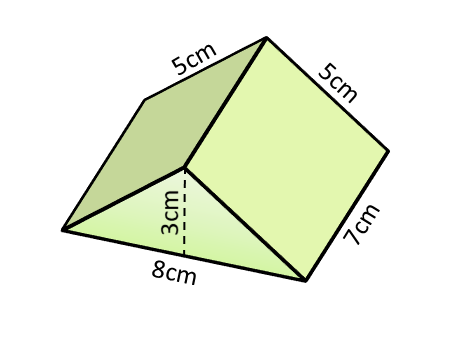
A right prism is a polyhedron that has two congruent and parallel faces (called the base and top), and all its remaining faces are rectangles. Recognize and identify rectangular prisms and pyramids, triangular prisms and. A polyhedron is a solid bounded by polygons.


 0 kommentar(er)
0 kommentar(er)
